АДАПТИВНЫЕ РЕГУЛЯТОРЫ №1 и №2
  НА НЕЙРОСЕМАНТИЧЕСКИХ СТРУКТУРАХ

Бодякин В.И., Чистяков А.А.

Рассматривается эволюционный подход построения интеллектуальных систем на базе нейросемантической сети. В качестве примера анализируется эволюционно усложняющийся нейросемантический регулятор для управления априорно неизвестным объектом. Рассматриваются теоретические и практические результаты каждого этапа конструктивного (эволюционного) развития регулятора. В результате анализа функционирования регулятора вводятся и теоретически обосновываются ряд понятий теории информации и саморазвивающихся (адаптивных) систем. Работа входит разделом в монографию "Общая теория эволюции информационных систем".

Москва 2005г.

ПРЕДИСЛОВИЕ

Исследуя возможности построения интеллектуальных информационных систем, наша группа вышла на нейросемантическую форму представления информации в виде многодольного иерархического графа. Предварительный экспертный анализ показал, что все исследованные нами задачи, решаемые человеком, могут быть разложены на элементарные функционально-топологические структуры многодольного графа. Для компьютерного моделирования и дальнейшей формализации свойства интеллектуализации была предпринята попытка собрать текстовую информацию об окружающем мире ребенка и ввести ее в разрабатываемую интеллектуальную информационную систему. Но оказалось, что тексты, представленные в учебниках "Родной речи" [ ] не полны (в силу многотиповости и сложности отношений между образами), а попытка расширить их до требуемой полноты приводила бы к непомерному росту компонент графа, что существенно усложнило бы анализ поставленной задачи.

В результате было предложено моделировать и исследовать интеллектуальные свойства человеческой психики на "простейших" задачах управления априорно неизвестным объектом - нейросемантическим регулятором. Анализ стал прозрачным, благодаря небольшому числу исследуемых компонент, а эволюционный подход позволял наращивать возможности интеллектуальных систем от простейших "безусловно рефлекторных" (случайно формируемых генетически эволюцией) до "интеллектуальных", использующих знание о предметной области, и даже до "разумных", когда процесс формирования знания осуществляется в самой технической (искусственной) информационной системе.

Сама же информационная система строится на базе нейросемантических структур. Основная их особенность заключается в том, что отдельным процессам (элементарным семантическим единицам) предметной области автоматически ставятся в соответствие образы-элементы) информационной системы. Автоматизация этого процесса основывается на минимизации битового ресурса физической структуры многодольного иерархического графа информационной системы по отношению к битовому ресурсу перерабатываемого текстового потока, идущего из предметной области. При этом, в графе автоматически получается структура, гомоморфная исходным причинно-следственным процессам предметной области. 

Данный процесс автоструктуризации, когда в каждой вершине многодольного иерархического графа, представленного нейроподобным N-элементом, посредством связей отображались семантические единицы предметной области, т.е. N-элемент ↔ семантическая единица, фактически формировал готовую структуру данных (процессов и объектов) произвольной предметной области для возможной автоматизации их обработки. А это уже открывает широкие горизонты для инженеров от информатики. Но помимо построения автоматизированных информационных систем появляется возможность и их эволюционного саморазвития, причем до достаточно высокоинтеллектуальных. Более формальные описания нейросемантической структуры, процесса ее формирования и характеристика свойств приведены в [ ].

Итак, перейдем к рассмотрению адаптивного регулятора на нейросемантических структурах для анализа и формализации различных проявлений свойств "интеллектуальности" в информационных системах.

Введение. Для управления все усложняющимися социальными и производственными процессами необходимы крупномасштабные интеллектуальные самонастраивающиеся системы управления, основой которых могут стать нейросетевые регуляторы. Для настройки нейросетевых регуляторов необходимо только задать классы состояний или режимов, определяемые, например, как: "нормальные" или "ненормальные" и, независимо от характера возмущений, такая система управления посредством внешних воздействий должна найти алгоритм по поддержанию на управляемом объекте процессов в нормальных режимах [1].

Фактически, при минимуме информации ("нормальное - ненормальное") и при возможности исследования вариантов управляющих воздействий (этап обучения), регулятор способен вывести управляемый объект в область нормальных режимов его функционирования при любых начальных допустимых условиях и при случайных возмущениях внешней среды. В общем случае, нейросетевой подход - это "размен" сложной алгоритмической процедуры некоторой задачи на распределенную структуру простых преобразований, решающих эту же задачу. При наличии на сегодня высокопроизводительного и дешевого hardware и дорогостоящего и инерционного труда программистов (software), нейросетевой подход открывает перспективы по широкомасштабной автоматизации широкого класса процессов, охватывающих практически все аспекты нашего жизнеустройства.

В работе рассматривается особый класс классических нейросетевых систем – нейросемантические структуры (НСС). В отличие от традиционных нейронных сетей, в НСС каждому нейроподобному элементу соответствует определенная семантическая единица исходного текстового потока¹ , что позволяет разработчику анализировать логику функционирования элементов системы в терминах языка предметной области. Второй существенной характеристикой НСС является ее ассоциативность. Более подробно о НСС можно посмотреть в [3, 4, 5] и http://www.ipu.ru/stran/bod/monograf.htm.

Построение теории нейросетевых адаптивных регуляторов весьма актуально как для технической сферы, так и для моделирования ими возможных механизмов в живых системах при поддержании ими гомеостаза в непрерывно изменяющихся средах.

Постановка задачи. Предположим, что состояние объекта зависит от вектора X (X = X¹, X², …, X^m, где m - число управляемых параметров-компонент объекта, его моделируемая размерность. Состояния объекта дискретны по каждой компоненте и равны N (N – максимальное значение числа состояний по какой либо из компонент). Соответственно, общее число состояний объекта (X_jⁱ) не превышает - N^m, что является пространством состояний объекта - S. S можно представить как m-мерный куб с ребром N.

Допустим, что в каждый такт времени (n) объект переходит из состояния X_n в состояние X_n+1 по некоторой функции перехода f, которая априорно неизвестна для адаптивного НСС-регулятора.

X_n+1  = f(X_n)                                                                    (1а)

Задавая случайным образом некоторое начальное X₀  (X₀ ∈ S, n=0), в соответствии с (1а), будет происходить дальнейшая эволюция внутренних состояний объекта, начиная траекторию его состояний.

Задача адаптивного регулятора заключается в подаче вектора управляющих воздействий F (F = F¹, F², …, F^m) на тех же значениях параметрах-компонентах, что и вектор X

X_n+1  =  f (X_n) + F_n ,                                                             (1)

таким образом, чтобы результирующее состояние объекта (X_n+1) как можно большее число тактов (n = 0,1,2,3,…, Ω, где:  Ω  >>  N^m ) находилось в области "нормального" режима (X_n+1 ∈ S). Число n - тактов   (X₁ = X₀, X₂, X₃, …, X_n) при которых объект не выходит из области "нормального" режима S определяет длину траектории управления.

Примем, что если длина траектории объекта управления превышает (N*N)^m тактов (пространство управления объекта), то будем считать такую траекторию положительной (нормальной), и считать, что регулятор научился управлять объектом при начальном (X₁ = X₀). Если же объект управления вышел из области S (попал в область Q - область "ненормальных" режимов) при  n < ( N*N)^m, то такую траекторию будем считать отрицательной и для наглядности будем обозначать ее последний такт символом "·".

Число отрицательных траекторий (область Q) определяется в соответствии с уравнением (1) как результирующее X_n+1,  выходящего за пределы "нормального" режима (X_n+1 ∈ S). В соответствии с конкретным уравнением (1) можно определить мощность множества отрицательных состояний управляемого объекта - M_Q.

Общее число состояний объекта, отраженных в его траекториях обозначим W (W ≤ (N*N)^m), мощность его определяется как объединение мощностей "нормальных" и "ненормальных" режимов (W = Q∪S,  Q∩S = 0).

Eсли для всех (X₀ ∈ S), число которых не меньше N^m, последние траектории являются положительными, то будем считать, что нейросемантический регулятор обучился управлять данным объектом.

Обучение регулятора можно построить как только на опыте отрицательных траекторий ("метод наказания"), так и только на опыте положительных траекторий ("метод поощрения"). При этом процесс обучения в этих двух случаях будет существенно отличаться. Одновременное использование "метода наказания" и "метода поощрения" дает качественно третий тип результата процесса обучения. В дальнейшем эти три случая будут рассмотрены на конкретном примере.

Напомним, что регулятор должен обучиться управлению состоянием любого объекта, поддерживая его в области S при произвольной детерминированной и априорно неизвестной функции переходов его состояний (f). Естественно, желательно, чтобы процесс обучения происходил за минимально возможное число пробных траекторий (число попыток, "число жизней") при произвольных начальных X₀ .

Для анализа результатов и построения теории адаптивного регулятора на нейросемантической сети необходимо уменьшить размерность задачи. Для этого примем m=1 (случай одномерного управляемого объекта) и число дискретных состояний выберем N=7. В этом случае "ручной" анализ функционирования адаптивного регулятора не вызовет никаких затруднений. В программной же реализации первой версии предусмотрены максимальные значения: m=10 и  N=10.

В качестве тестового примера управляемого объекта будем рассматривать упрощенную физическую модель (см. рис. 1), аналогичную часто рассматриваемой задаче "обратного маятника", используемую в качестве теста для классических нейронных сетей [2].

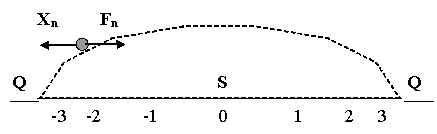Рис. 1.

Безынерционный объект находится на выпуклой поверхности S. Под действием силы "тяжести" f (см. уравнения 1 и 2) он стремится скатиться с этой поверхности. Задача системы управления заключается в том, чтобы воздействиями F_n удержать его на выпуклой поверхности. Начальные значения положения шарика X₀  (-3 ≤ X₀ ≤ 3). Состояния S(X_n = {-3, -2, -1, 0, 1, 2, 3}. Состояния Q (X_n < -3  и  X_n  > 3). В качестве примера опишем изменение состояние шарика под действием "гравитационных" сил как:

X_n+1 =  2*X_n                                                                          (2)

Состояния переходов данной физической модели выражается следующим графом:

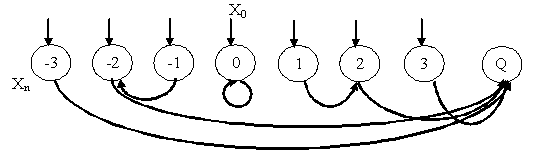Рис. 1a.

Для последующего теоретического исследования механизмов самоорганизации системы управления на нейросемантической сети мы еще более упростим и физическую модель, см. рис. 2.

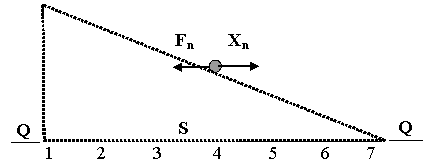Рис. 2.

Безынерционный объект находится на наклонной поверхности S. Под действием силы "тяжести" f (см. уравнение 3а) он скатывается вправо за каждый такт (от n  до  n+1) на одну единицу. 

X_n+1  =   1 + X_n                                                                      (3а)

Задача системы управления F удержать его в области S при произвольных начальных условиях X₀ и при малом случайном возмущении среды Z. Введение в уравнение малого случайного воздействия Z необходимо для приближения модели регулятора к реальным процессам, а также для избежания попадания управления регулятора в устойчивые периодические траектории (например, для уравнения 2, при X_n=0 и Fsub>n =0).

Начальные значения положения объекта X₀ (1 ≤ X₀ ≤ 7). Состояния S(X_n) = {1, 2, 3, 4, 5, 6, 7}. Состояния Q (X_n < 1  и  X_n > 7). Силы, действующие на состояние объекта, опишем как: X_n+1 =   1 + X_n - "силы гравитации в вязкой среде"; F_n - управление регулятора (F_n = {-1, -2, -3, -5, -6, -7}); Z_n - малое случайное возмущение внешней среды (max |Z_n |<< max |F_n|,  Z ≈ 0, ±1, ±2).

X_n+1 =   1 + X_n  +  F_n  + Z_n                                                           (3)

Рекуррентное уравнение (3) в гносеологическом плане существенно проще (2), на что указывают и данные из зоологии. Например, задачу затаскивания-закатывания объекта в некоторое место выполняют уже насекомые, тогда как балансировать объектом способны только высшие животные (дрессированные дельфины, морские котики и др.). Поэтому теоретический анализ мы будем проводить с объектом, описываемым уравнением (3), а для практического тестирования качества функционирования нейросемантического регулятора будем использовать объект, описываемый уравнением (2), а также любым другим (3b) при условии наращивания необходимой для этого вычислительной мощности регулятора.  

X_n+1 =   f(X_n)  +  F_n  + Z_n                                                        (3b)

В общем случае функцию перехода (изменения) состояний управляемого объекта будем описывать в табличной или графовой форме. Так, уравнение (3а), отображающее изменения внутреннего состояния объекта в табличной или графовой форме, будет выглядеть следующим образом:

В нашем случае переход состояний объекта под действием силы тяжести f будет: a₁ → a₂, a₂ → a₃ , a₃ → a₄, a₄ → a₅, a₅ → a₆, a₆ → a₇, a₇ → a_Q  (см. рис. 3). При этом, в соответствии с рис. 2, примем: a₁ =1, a₂ =2, a₃ =3, a₄ =4, a₅ =5, a₆ =6, a₇=7 .

Область определения "нормальных" S состояний X = { a₁, a₂, a₃, a₄, a₅, a₆, a₇}, остальные состояния Q, при которых X ≠ { a₁, a₂, a₃, a₄, a₅, a₆, a₇}.

Область значений управляющих воздействий F в нашем случае определим как область "нормальных" S состояний X со знаком минус, F = ≠{ a₁, a₂, a₃, a₄, a₅, a₆, a₇}. На область значений F накладывается ограничение: для любого X_n  (X_n ∈ S) должно существовать F_n такое, что f(X_n ) + F_n+ Z_n также принадлежит S.

Область значений "ненормальных" состояний объекта Q(X_n+1 = 1+X_n + F_n + Z_n < 1  и  X_n+1 = 1+X_n + F_n + Z_n ≤ 7) совместно с областью "нормальных" состояний объекта S (1≤ X_n+1 = 1+X_n + F_n + Z_n    ≤7) представлены в таблице 1.

Таблица 1.

Также сделаем предположение, что для адаптивного НСС-регулятора  №1 все значения  состояний X = { a₁, a₂, a₃, a₄, a₅, a₆, a₇} объекта независимы.

Мощность (M) числа состояний S равна M_S = (N² + N) / 2, Q, соответственно, равна  M_Q  = ((N-1² +N-1) / 2, что при принятом N=7, M_S = 28 и M_Q = 21. M = (N *N)sup1  = N² = M_S + M_Q  = 28 + 21 = 49.

Отметим, что M_S ~  M_Q ( M_S =  M_Q + N). Эта оценка примерного равенства мощностей множеств S и Q будет нам удобна при оценке вероятностей случайного формирования траекторий.

На рисунке 4 представлен фрагмент графа состояний управляемого объекта в состоянии X_n = a₃. Этот фрагмент полностью соответствует описанию таблицы 1 в 3-й строке.

Воздействие F_n = a₁ (-1) на исходное значение состояния объекта X_n = a₃, соответствующего величине 3, переводит объект в сам себя X_n+1 = a₃  (1+3-2= 3); воздействие a₂: X_n+1(a₂) = 1 + X_n (a₃ + F_n(a₂)  = 1 + 3 -2=2; воздействие a₃: X_n+1(a₁) = 1 + X_n(a₃) + F_n(a₃)  1 + 3 -3=1; воздействиями a₄, a₅, a₆, a₇: X_n+1(Q) = 1 + X_n(a₃) + F_n(a₄, a₅, a₆, a₇) = 1 + 3 - 4, 5, 6, 7 < 1, что соответствует состоянию объекта области Q. Аналогично и для всех остальных состояний объекта X_n (a₁, a₂,  a₄, a₅, a₆, a₇) воздействия Fn (-(a₁, -a₂, -a₃, -a₄, -a₅, -a₆, -a₇) переводят состояние объекта в области Q или S.

Мы рассмотрели механизмы описания объекта и возможное взаимодействие с ним управляющего регулятора. Перейдем  к описанию структуры адаптивного регулятора, построенного на нейросемантической сети.

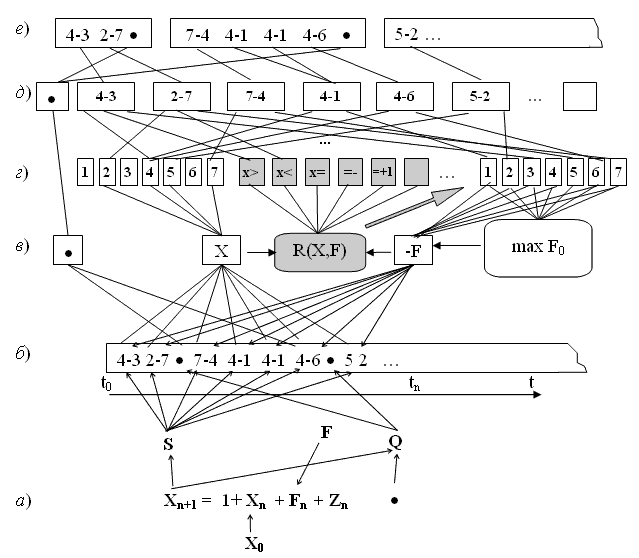
Схема адаптивного регулятора №1 на нейросемантической сети. В качестве системы управления рассмотрим адаптивный регулятор на нейросемантической сети, см. рис. 5.

Это двухслойная нейросеть (слои д и е, см. рис. 5) с функционально упрощенными нейроподобными N-элементами [3]. Основное их отличие от классических нейронов [1] с алгебраической суммацией сигналов на входе заключается в векторной (пространственно-временной) обработке входных сигналов. Механизм функционирования N-элементов станет ясным из описания алгоритма настройки рассматриваемого адаптивного регулятора.

Пример механизма изменения состояний объекта (X_n) отображен на уровне а рисунка 5. На уровне б отображен протокол изменения состояний объекта и управляющих воздействий регулятора (F_n). Протокол привязан к дискретной временной оси  (t_n). Алфавит протокола состоит из N+2 знаков (1, 2, 3, 4, 5, 6, 7, -, ·).  Грамматика формирования протокола – это последовательность попыток обучения, каждая из которых, это последовательность пар (X_n F_n) завершающаяся знаком - "·". Если же длина последовательности пар превышает некоторую длину (например, равную N₂ ~  2*M_S), то она рассматривается как положительный результат обучения, и при обучении "методом наказания" в памяти регулятора может не отображаться.

На уровне в отображены компоненты процесса: состояния объекта (X_n),  воздействий регулятора (F_n), завершения i-й попытки (·), а также механизм блока управляющего воздействия (блок max F0, см. рис. 5). Работа блока заключается в выборе элемента из F-группы элементов уровня г с максимальным значением некоторой величины U(n), которая количественно отражает величину меры "близости к наказанию", т.е. к "·", вычисляемую на N-элементах.

На уровне г отображены две группы элементов алфавита, отображающие значения состояния объекта (X_n) и воздействия регулятора (F_n). Эти элементы выполняют функцию простейшей ассоциативной коммутации различных пар (X_n F_n) для N-элементов слоя д при реализации конкретных попыток обучения регулятора.

Уровень д – это первый слой N-элементов нейросемантической сети адаптивного регулятора. N-элементы этого слоя имеют два входа, для компоненты X_n состояния объекта (1-й вход) и для F_n ответного воздействия регулятора (2-й вход). Это слой ассоциативных N-элементов, отображающих простейшие "условные рефлексы" регулятора. В нем находятся только различные (уникальные) пары (X_n F_n). Если в протоколе встречаются тождественные пары, например, "4-1… и 4-1", то они отображаются только одним N-элементом с информационным содержанием "4-1". Каждая же новая реализация пары, тождественная информационному содержанию N-элемента, только добавляет ссылку (связь) с N-элементом вышележащего слоя (уровня е), отображающим конкретную попытку обучения. Общее число N-элементов д слоя не превышает N^m2.

N-элементы уровня е имеют число входов, равное числу пар (X_n F_n) в каждой попытке обучения. Завершающая пара формируется либо при попадании X_n в множество состояний Q (сигнал - "·", это дополнительный вход, показанный на рис. 5 и приведен лишь для большей иллюстративности материала) либо, если число пар превышает заданное N² – "положительная траектория". Новый N-элемент уровня е формируется из резервного N-элемента (самый правый свободный в слое). Сигналом к формированию нового N-элемента служит появление завершающей пары. Резервный N-элемент имеет практически бесконечное число входов.

Свойство слоев N-элементов адаптивного регулятора таково, что в каждом N-элементе содержится ровно одна семантическая единица своего иерархического уровня ("условный рефлекс" как конкретная пара X_n F_n - слой д, или конкретная траектория – в слое е). Семантическая единица представляет последовательность знаков в рамках алфавита объекта (1, 2, 3, 4, 5, 6, 7, -, ·). Свойство соответствия семантической единицы в конкретном физическом отображении (N-элемент) чрезвычайно важно в адаптивных информационных системах, поэтому это свойство и подчеркивается в его названии - нейросемантический. Более подробно этот аспект рассматривается в [3].

Алгоритм функционирования адаптивного регулятора №1. Рассмотрим динамику функционирования адаптивного регулятора на основе нейросемантической сети.

Результаты экспериментов с моделью №1 адаптивного регулятора  подтвердили ожидаемые аналитические расчеты. Так, при мощности M_S ~ M_Q вероятность (р) завершения траектории, т.е. попадания пары (X_n F_n) в область Q,  в начале процесса обучения регулятора в зависимости от числа шагов траектории (n) велика и имеет следующий числовой вид: n=2, p=0.50;  n=4,  p=0.88; … n=8,  p=0.99; Соответственно, этим и объясняются короткие начальные траектории в экспериментах (см. рис. 6).
На этапе завершения обучения (число попыток ~ MQ) длины траекторий должны несколько возрастать, но ненамного. Вероятность (р) того, что регулятор сможет построить траекторию длиной до N* пар (X_n F_n) при последней ненайденной паре (X_n F_n) из области Q равна р ~ 0.007. Таким образом, при числе попыток M_W (M_W = N2  = M_S + M_Q) вероятность нахождения всех пар (X_n F_n) области Q и запоминания их регулятором в форме N-элементов уровня д порядка р ~ (1 - 0.00005). Следовательно, за M_W  обучающих траекторий адаптивный регулятор на нейросемантической сети способен обучиться и устойчиво поддерживать (р>0.9999) объект в области S.
Необходимо отметить, что данная оценка времени обучения семантического регулятора применима только при обучении "методом наказания". Так, при обучении "методом поощрения" регулятор быстрее выходит на траектории длиной в N* пар ("обучается" при определенных начальных условиях X0), но зато на M_W-й попытке обучения вероятность довести длину траектории до  N* пар (X_n F_n) существенно меньше, чем при обучении "методом наказания". Это как бы два "психологических" типа регулятора: "мальчишечий" и "девчоночий". Первый сначала попадает во все возможные неприятности, но зато потом уверенно чувствует себя в данной среде. Второй тип старается придерживаться найденных решений, но общая длительность процесса обучения возрастает. Эти два тапа стратегии обучения регулятора можно использовать в зависимости от характера задач.
В ходе экспериментов (обучение "методом наказания") с объектами, приведенными на рис. 1 и 2, а так же с объектами со случайно заданными парами переходов состояния  (X_n → X_n+1 ), во всех 300 экспериментах  (по сто на каждом типе объектов) адаптивный регулятор настраивался на рабочий режим (успешно обучался) за M_W попыток.
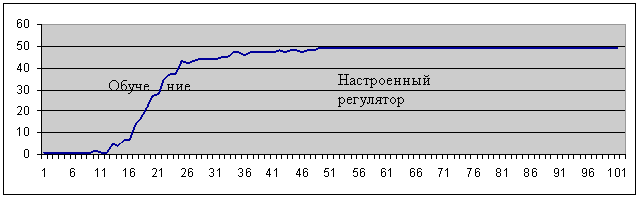
На графике 1 приведен пример типичного вида графика при обучении регулятора (на объекте, приведенном на рис. 1). На оси ординат отложена усредненная длина траектории, и по оси абсцисс - число  экспериментов (100).

График 1.

На рис. 6 приведены результаты фрагментов протоколов экспериментов по управлению объектом, приведенного на рис. 2 и описываемого уравнением (3), и виды исходных данных, задающих управляемый объект для программы адаптивного регулятора.
1.  1 -7  ./-5  -- 1          Обозначения (структура траектории):
2.  3 -5  ./-1  -- 1                  n. - номер траектории;  
3.  6 -6   1 -4  ./-2  -- 2         пары  (Xn  Fn)…; 
4.  1 -6  ./-4  -- 1                  ./(Xn+1) - завершение траектории; 
5.  3 -4  ./0  -- 1                   -- (k),++(k)  -  результат и число пар в траектории; 
…                                        - случайные возмущения Zn(0,1,2) на каждой пятой паре траектории

Форма задания исходных данных для исследований адаптивного регулятора (см. рис.2).
N= 7                                                   - число нормальных состояний объекта и пар переходов;
(1 2)(2 3)(3 4)(4 5)(5 6)(6 7)(7 8)       - пары (Xn  Xn+1) отражают переходы состояния объекта

Xn  → Xn+1  

- область нормальных состояний объекта – первый элемент

пары S ( Xn Xn+1>) = {1, 2, 3, 4, 5, 6, 7};
F= -1 -2 -3 -4 -5 -6 -7                        - возможные управляющие воздействия регулятора;
N= 13
(0 1)(1 2)(2 4)(-1 -2)(-2 -4)(3 6)(-3 -6)(4 8)(-4 -8)(-5 -10)(5 10)(-6 -12)(6 12)
F= -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Результаты экспериментов с моделью адаптивного регулятора, представленного на  рис. 2, показали, что состояние объекта (X_n F_n) только один раз попадает в область Q (запрещенная область). Причем во все состояния области Q, управляемый объект "обязательно" попадет, т.к. исходное состояние X_n = X₀, где X₀  задается случайно из области  X₀  (1 ≤ X₀ ≤7)

Количество Q состояний для случая (2) равно ~ N*N/2. Перебрав их в начальном состоянии функционирования регулятора, система переходит в устойчивое управляемое состояние.  При любых начальных значениях X₀(X_n  = X₀), и случайной компоненте Z (3), такой, что ее добавление не выводит X_n в область Q, модель данного адаптивного регулятора может неограниченно долго поддерживать состояние управляемого объекта в области S.

Эксперименты по заданию функции по (1) и со стохастическими переходами, представленными в табличной форме (при 3 < N < 21) показали, что данный регулятор для любой из данных функций после обучения (прохождения всех состояний Q) стабильно поддерживает объект управления в области S.

К положительным характеристикам адаптивного регулятора можно отнести:

• -  возможность работы с любым объектом (см. рис. 1,2), функция перехода состояний которого априорно неизвестна и заданы только списки положительных S и отрицательных Q состояний объекта. Для некоторых типов задач это могут быть единственные данные;
• - период обучения (настройки) регулятора четко выделен и локализован на начальном этапе его взаимодействия с объектом;
• - после этапа обучения регулятор уже не допускает ни одной ошибки в процессе управления состоянием объекта, только один раз попадая в область Q ("не наступает на грабли более одного раза");
• - допустима работа с объектом, у которого функция перехода состояний может медленно "дрейфовать", регулятор будет подстраиваться в процессе эксплуатации;

Данный тип регулятора может иметь прикладную значимость дляобъектов управления с неизвестными функциями переходов их состояний, когда известны только область Q. Под этот класс задач подпадает достаточно много объектов управления (космические объекты, объекты в агрессивных средах и пр.).

К нежелательным характеристикам данного типа регуляторов можно отнести обязательный проход всего пространства состояний объекта (X*F). Для практических задач, когда число значений параметра N может измеряться тысячами, а размерность задачи сотнями и тысячами параметров, декартово пространство состояний объекта может измеряться величиной в 10100, что для современной вычислительной техники недопустимо. Поэтому, зная способности биологический нейронных сетей к обобщению, абстрагированию и другим интеллектуальным функциям, существенно уменьшающим пространство перебора, необходимо модифицировать модель адаптивного регулятора представленного на  рис. 2, чтобы он смог преодолеть возникающее "проклятие размерности", сведя пространство перебора до "практических величин", не превышающих ~ 1010. Это чрезвычайно важная и актуальная проблема, которую необходимо решить для широкого практического внедрения рассматриваемого регулятора.

Модификация нейросемантического регулятора. Так глядя на задачи, представленные на рис. 1 и 2, человек может легко, только на основе ранее полученных знаний, обойти полный перебор и, независимо от N, найти решение этих задач. Так, для задачи, представленной на рис. 2, при любом X_n решением является F_n = -1 или - X_n ≤-F_n ≤ -1, практически сводящееся к  F_n = -1. Для задачи, представленной рис. 1, решением является противоположная направленность воздействия F_n = - X_n и одновременно большее по модулю значени F_n|≥|- X_n|. Видно, что найти второе решение существенно сложнее первого решения(F_n = -1 при любом X_n).  Задача же управления объектом со случайно заданными парами переходов состояния (X_n → X_n+1 ), естественно, никакими приемами лучше, чем перебор, решена быть не может, но, к счастью, на практике такие задачи либо маломерны, либо выясняется, что для них находится свое причинно-следственное пространство (пространство R-отношений).
Образование человеку дает абстрактные понятия ("равные", "большие", "натуральный ряд", "число"), которые позволяют ему решить вышеприведенные задачи (рис. 1 и 2), минуя метод "проб и ошибок". Предварительно исследуя объект, человек относит его к одной из известных ему моделей и затем, в соответствии с этими моделями, начинает применять известное ему знание. При этом, как показывает практика, отступает ужасающая размерность прохода всего пространства состояний объекта (X*F) методом "проб и ошибок". В этом направлении и необходимо модифицировать нейросемантический регулятор.

Адаптивный нейросемантический регулятор №2. В слой г адаптивного регулятора (см. рис. 5 и 7) можно вставить группу нейронов-рецепторов, которые будут отражать некоторое своеобразное "начальное образование" регулятора. Каждый из этих нейронов-рецепторов будет переходить в активное состояние (U(n)=1.0), если текущие значения X_n  F_n будут соответствовать некоторым R-отношениям: "модуль F_n больше модуля X_n", "модуль F_n меньше модуля X_n", "F_n одного знака с X_n", "F_n разных знаков с X_n",  "модуль F_n равен модулю X_n", "-F_n  равна X_n", "-F_n равна X_n+1", а также величин и знаков их производных X_{n -1} = ΔX, F_n - F_n-1 = ΔF и прочих возможных отношений.

Введение в слой г нейронов-рецепторов "начального образования" с вышеуказанными свойствами R-отношений будет эквивалентно некоторому "простейшему образованию по теории чисел" адаптивного нейросемантического регулятора. Такой регулятор с группой нейронов-рецепторов будем называть адаптивным нейросемантическим регулятором №2, см. рис. 7.

Отметим, что введение в слой е нейронов-рецепторов (R-отношений) не ориентировано ни на какую конкретную задачу, они вводятся как бы "про запас". Предполагается, что одного-двух десятков задействованных нейронов-рецепторов будет достаточно для покрытия особенностей всех управляемых объектов рассматриваемого типа. Излишние же нейроны-рецепторы не будут ухудшать качество обучения регулятора №2 относительно регулятора №1. Те же нейроны-рецепторы, которые будут отражать особенности конкретного объекта (X_n+1 = f(X_n)), будут способствовать более эффективной настройке регулятора на этот объект, нежели чем простой перебор. Если же некоторые свойства объекта не будут отражены в нейронах-рецепторах (например, для негладких функций f(X_n)), то качество обучения регулятора №2 просто не будет лучше, чем у регулятора №1.

Структурная схема адаптивного нейросемантического регулятора №2, в отличие от регулятора №1 изменяется мало. Добавляется лишь блок вычисления отношений R(X_n,F_n) (слой в), который формирует связи между нейронами-рецепторами и элементами блоков X и F слоя г . Блок  вычисления отношений X_n и F_n строится перебором всевозможных пар X_n, F_n. Для малых значений N это вполне приемлемо.

В процессе идентификации X_n (по алгоритму №1), сформированная отрицательная величина U(t) (обучение "методом наказания") с N-элементов слоя е передается по сформированным в процессе обучения связям на N-элементы слоя д. Далее, величина параметра U(t) по дополнительным связям N‑элементов уровня д, сформированных блоком вычисления отношений X_n и F_n,  передается ниже на нейроны-рецепторы уровня г, которые рассылают ее на все элементы F, соответствующие условиям на нейронах-рецепторах текущего R‑отношения Xn и Fn. Например, если активируется нейрон-рецептор "модуль F_n больше модуля X_n", то на все  F_n , удовлетворяющие этому признаку относительно текущего X_n , посылается дополнительная отрицательная добавка U(n). Затем, эта дополнительная величина U(t) полученная от блока нейронов-рецепторов, складывается с величиной U(t), получаемой в результате работы алгоритма №1. Потом выбирается F_n с максимальным значением величины U(t). Далее, все как по алгоритму №1. Т.е., по алгоритму №2 активация N-элементов с уровня е передается на F_n как непосредственно по алгоритму №1, так и через блок вычисления отношений (двойная стрелка, см. рис. 7).

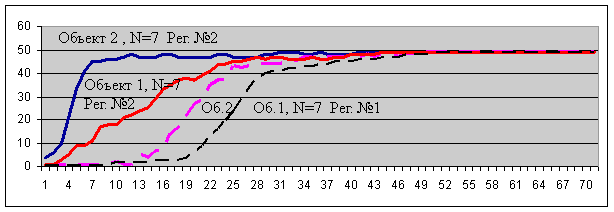
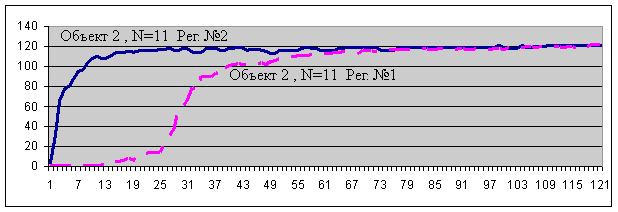
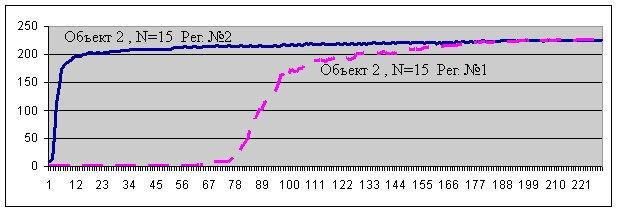
Результаты экспериментов с моделью адаптивного регулятора №2 показали, что для устойчивого обучения регулятору №2 необходимо существенно меньшее число попыток (траекторий), чем для регулятора №1 (напомним, что для обучения регулятора №1 необходимое число траекторий ~ N*N, и за это время он должен попасть во все пары X_n F_n, принадлежащие M_Q). При этом, для регулятора №2 наблюдается лишь незначительный рост числа попыток с ростом N. Результаты экспериментов для модели (рис. 2) представлены на графике 2.

График 2.

а).

б)

в)

Это примеры типичных графиков для адаптивного регулятора №2 в сравнении с регулятором №1. Из графиков видно (по оси абсцисс отложено число попыток обучения, по оси ординат –  длина правильных попыток-траекторий), что эффективность регулятора №2 почти не зависит от N (N=7,11,15), тогда как у регулятора №1 она почти квадратичная от N.  На графике 2а также видно, что эффективность управления регулятором №2 объектом 2 (см. рис. 2) выше, чем объектом 1 (см. рис. 2), тогда как для регулятора №1 эффективность управления обоими объектами равна и определяется M_Q, что и было выше объяснено теоретически.

Анализ результатов экспериментов с моделью адаптивного регулятора №2 показал, что  регулятор №2, как и регулятор №1, перебирает все пространство состояний. Только если у регулятора №1 это одно пространство состояний  (X*F), то у регулятора №2 дополнительно появляется и пространство R-отношений (R(X, F). Обычно пространство R-отношений существенно меньше пространства состояний объекта (X*F). Перебрав всевозможные R-отношения (R(X,F)), регулятор №2 настраивается на управление объектом. Следовательно, число тактов обучения регулятора №2 определяется минимальной размерностью пространства состояний  (X*F) или пространства R-отношений (R(X , F)):

M2_Q = min{(X*F),(R(X,F), (R(X,F))                                                  (4)

Выводы. Для модели адаптивного регулятора №2 видно существенное уменьшение числа коротких ("ненормальных") траекторий обучения (M2Q) относительно MQ. Так как R‑отношения (R(X,F)) не зависят от числа состояний (дискретности) объекта (N), то чем больше N, тем относительно большая эффективность алгоритма  №2, т.е. для выхода на устойчивый режим управления в названных задачах, потребуется уже существенно меньшее число траекторий для обучения, чем MQ.

M2Q / MQ →  0,                                                                (5)

при N→ ∞                                                                             

Этот результат показывает, что при наличии в блоке отношений нейронов-рецепторов (см. слой г  рис. 7), которые частично или полностью (как одним нейроном-рецептором так и их совокупностью) отображают априорно неизвестную функцию f состояний перехода  управляемого объекта ("общее образование"), процесс настройки регулятора по эффективности не уступает человеку (что подтверждается экспериментами, когда для нескольких типов объектов в качестве управляющего регулятора выступали студенты).
Экспериментальные исследованиях адаптивного регулятора с переходом на "метод поощрения" (целевое состояние объекта), как и с одновременным рассмотрением двух областей состояний Q+ и  Q-, показали еще большую эффективность обучения регулятора, но в силу повышенной сложности теоретического анализа этих режимов в рамках этой статьи их результаты не анализировались.   

Практическое применение модели адаптивного регулятора №2 возможно для широкого класса задач, если они имеют гладкие функции переходов состояния объекта. Это управление объектами в малоизвестных или сложных и агрессивных средах (планетоходы, роботы манипуляторы, адаптивные спутники и др.), а также обработка и кластеризация больших слабоструктурированных информационных потоков (работа с текстовой информацией, прогнозирование временных рядов и пр.).

Естественно, что при этом в блоке вычисления отношений X_n и F_n должны существовать некоторые нейроны-рецепторы, которые всегда реагируют, когда объект попадает в область Q, и не реагируют, если объект попадает в область S. Этот механизм аналогичен формированию абстрактных понятий, что сделает эффективность обучения адаптивного нейросемантического регулятора практически независимым от N (числа значений  параметра).

Образование таких нейронов-рецепторов может осуществляться в модели случайно, а может и под действием внутренних механизмов регулятора (адаптивный нейросемантический регулятор №3), в частности, в зависимости от величины текстовой энтропии [3]. Но это задача следующего этапа исследования и развития теории  адаптивного нейросемантического регулятора.

СПИСОК   ЛИТЕРАТУРЫ

1. Уосермен Ф. Нейрокомпьютерная техника. М.: Мир. 1992. – 240 с.
2. Sutton R.S., Barto A.G. "Reinforcement Learning: An Introduction". MIT Press, 1998:  http://www-anw.cs.umass.edu/~rich/book/the-book.html
3. Бодякин В.И., Куда идешь, человек? (Основы эволюциологии. Информационный подход). - М. СИНТЕГ, 1998, 332с.   http://www.ipu.ru/stran/bod/monograf.htm
4. Бодякин В.И. Информационные иерархически-сетевые структуры для представления знаний в информационных системах. //Проблемно-ориентированные программы. Модели, интерфейс, обучение: Сб. трудов. – М.: Институт проблем управления, 1990.
5. Бодякин В.И., Чистяков А.А. Ассоциативные информационные структуры и модели памяти, - в сб. Проблемы информатики - материалы конференции "От истории природы к истории общества: "Прошлое в настоящем и будущем", М., 2003.

Для замечаний