АДАПТИВНЫЙ  РЕГУЛЯТОР  №3
НА  НЕЙРОСЕМАНТИЧЕСКИХ  СТРУКТУРАХ

("РАЗУМНЫЙ  РЕГУЛЯТОР")

На адаптивном  нейросемантическом  регуляторе  №3 показано самоформирование отношений (т.е. свойство разума), задаваемых ранее в адаптивном  регуляторе  №2 извне. Это свойство регулятора теоретически разрешает проблему построения искусственного разума и позволяет на регуляторе №3 исследовать все особенности искусственного разума и интеллекта.

ПРЕДИСЛОВИЕ

В работе "Адаптивные регуляторы №1 и №2 на нейросемантических структурах" Бодякина В.И. и Чистякова А.А. были проанализированы два типа адаптивных регуляторов на нейросемантических структурах, регулятор №1 и регулятор №2.

На регуляторе №1 была показана возможность его самообучения по управлению любым априорно неизвестным объектом за счет перебора всего пространства его состояний (аналог универсальной адаптируемости живого). На регуляторе №2 продемонстрировано такое характерное свойство интеллекта как практическое преодоление "проклятия размерности" в "гладких" пространствах состояний управляемых объектов. За счет предварительного обучения возможным различным отношениям ("школьное образование", примеры отношений: управляющее воздействие больше/меньше состояния объекта, воздействие и состояние одного/разных знаков и др.), при взаимодействии регулятора с предметной областью скорость обучения практически не зависела от размерности пространства состояний управляемого объекта.

Задача этой работы - показать на регуляторе №3 процесс самоформирования отношений (т.е. свойство, которое можно отнести к свойству разума биологических систем, в частности, человека), изначально задаваемых в регуляторе №2 извне. Это свойство регулятора №3 теоретически разрешает проблему построения искусственного разума и позволяет на примере регулятора №3 формально исследовать все особенности искусственного разума и интеллекта.

Введение. Задача нейросемантического регулятора №3 (НСР №3), как и раньше у регуляторов №1 и №2 [  ], будет заключаться в поддержании произвольного объекта f(X) системой управляющих воздействий F его в области нормальных состояний S = { X_a, X_b, X_c ,  … , X_w } при произвольных начальных условиях X₀ и при малом случайном возмущении среды Z (см. 1).

Xn+1 =   f(Xn ) +  Fn  + Zn                                                            (1)

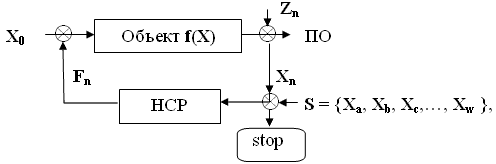
Рис. 1.

Естественно, что особенности и различия управления заключаются в самих нейросемантических регуляторах: №1, №2 и №3. Кратко рассмотрим эти особенности.

Так, в регуляторе №1 (НСР  №1) при формировании управляющих воздействий Fn учитывались только конкретные пары (X,F), которые и составляли "предложения" (X_k,F_l; X_m,F_d; X_k,F_y; …  X_Z,F_k; E±) с "точкой" (E±). Обработка пар НСР №1 была примитивной: если пара X_Z,F_k; приводит к X_n+1 ∉ S, то  "предложение" завершается отрицательной "точкой" E- и парыX_Z,F_k в будущем надо избегать, т.е. при X_n+1  = X_Z  никогда не давать F_k . Если же управление F_n таково, что число пар в "предложении" превышает некоторую величину (например, число всевозможных состояний пар X,F;), то для регулятора следует, что пары ("эвристики", "условные рефлексы") из этого предложения безопасны и их можно (надо) повторять при формировании будущих управляющих воздействий F_n .

Этот логически простая схема управления априорно неизвестным объектом, фактически сводящая к перебору всевозможных пар (X,F), образует в самом НСР №1 алгоритмически прямой поток управляющих воздействий, см. рис. 2.

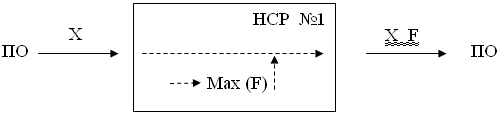
Рис. 2.

В отличии от НСР №1,  в НСР  №2 значения текущих пар (X,F;) связывались с уже предварительно полученными регулятором отношениями R(X,F), которые уже участвовали при формировании управляющих воздействий F_n помимо самих значений пар. Логическая схема выбора становилась более сложной, но в результате могло произойти существенное сокращение перебора пространства состояний системы "Объект-НСР" (число всевозможных состояний пар X,F; в этой системе), см. рис. 3.

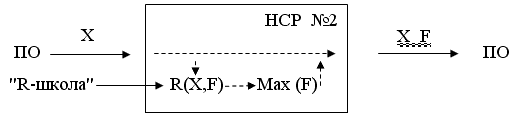
Рис. 3.

Это сокращение происходило всегда, когда практически реализуемое (в процессе функционирования) пространство отношений R(X,F) было меньше пространства состояний системы "Объект-НСР". На практике это достаточно частая ситуация, которая определяется качеством "R-школы", см. график 1.

График 1

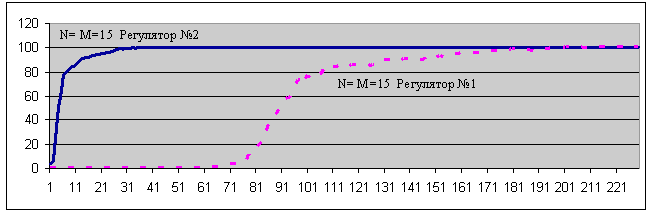
На графике 1 представлен типичный пример соотношения скоростей обучения для адаптивного регулятора №2  и регулятора №1. На графике (по оси абсцисс отложено число попыток обучения, по оси ординат – % правильных попыток-траекторий регулятора) видно, что эффективность обучения регулятора №2 много лучше чем у регулятора №1. Экспериментально показано, что при настройке управления на однотипные объекты, скорость обучения регулятора №2 почти не зависит от размерностей N и M (N – число состояний объекта, M – число состояний возможного управления, в эксперименте для простоты принималось N = M = 15, 17,19, 21), тогда как у регулятора №1 она квадратичная (N*M – мощность пространства числа состояний регулятора). Т.е., пример регулятора №2 демонстрирует возможность практического преодоления "проклятия размерности".

Постановка задачи. Построить нейросемантический регулятор №3 таким образом, чтобы в нем только на основании физических свойств его элементной базы, а также физических характеристик самого управляемого объекта,  происходило (естественное) самоформирование всевозможных R‑отношений, как, например, представленных в регуляторе №2.

Так, на нейросемантическом регуляторе №1 можно продемонстрировать свойство – "целенаправленность жизненности", как возможность адаптироваться под любую ПО; на регуляторе №2 – "интеллектуальность", как возможность существенного сокращения перебора; и на регуляторе №3 необходимо показать "разумность", как целенаправленное (само)порождение нового знания.

Тем самым, на базе нейросемантических регуляторов №1, №2 и №3 было бы подведено теоретическое основание для инженерного построения искусственного разума (ИР),  т.е. теоретически удалось решить (закрыть) проблему построения ИИ. Как и вычислительная техника, которая начала развиваться с теоретических моделей "машин Тьюринга и Поста", так и анализ работы нейросемантических регуляторов может способствовать формированию широкого фронта научных работ по разработке ИР.

Нейрокомпьютинг. До сих пор основным конструктивным элементом современного нейрокомпьютинга является формальный нейрон МакКаллока-Питса 1943года [ ] см. рис. 4.

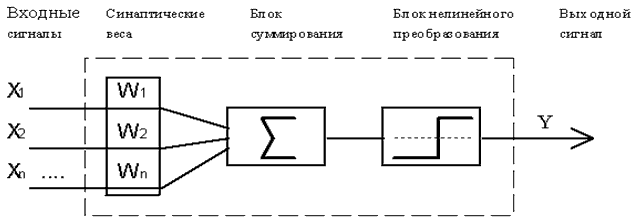
Рис. 4.

Это простейший пороговый сумматор с n входами и одним выходом. В блоке суммирования происходит накопление общего входного сигнала, равного взвешенной сумме входов 

net = Σⁿ_i=1 X_i * W_i.                                                              (2a)

Если сумма сигналов на входе превышает некоторый порог Q, то на выходе Y появляется активность, или 1. В остальных случаях на его выходе 0 [ ].

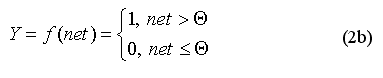
Элементная база НСР. Нейроподобный N-элемент НСР отличается от классического формального нейрона тем, что он работает уже с векторными  величинами - это совокупный пространственно-временной вектор (тензор).

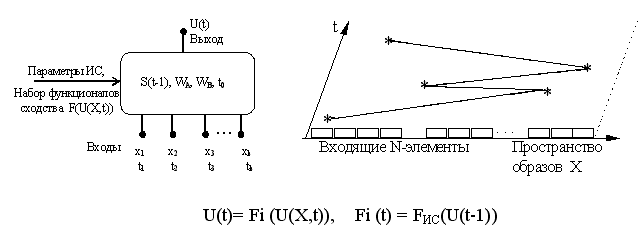
Рис. 5.

Если на вход N-элемент поступит такой же пространственно-временной вектор как и при его формировании (включение через связи в память НСР), то выходе появляется активность = 1*. Если же на входе N-элемента пространственно-временной вектор будет отличаться от "запаянного" в него, то на выходе будет величина активности в пределах от 0* до 1*. Причем она будет отражать контекстную (ассоциативную) близость этих векторов.

Схемами на базе из N-элементов можно моделировать любые логические схемы, включающие "и", "или", "не", но основное их предназначение - это структурированное хранение подпоследовательностей текстовых форм (пар X,F;), в которых уже необходимо отображать причинно-следственные связи.

Из N-элементов можно образовать послойные структуры (см. рис. 6), открывающие возможность иерархического построения памяти ИС. И сама входная информация образует слева-направо и снизу-вверх связи на свободных  N-элементах, тем самым отображаясь в нейросемантической структуре. Это второе важное свойство элементной базы НСР.

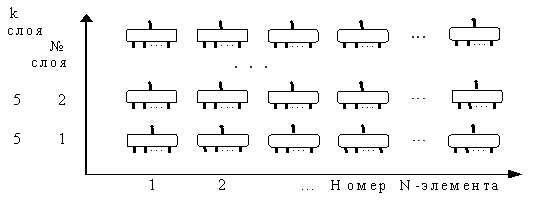
Рис. 6.

В процессе образования связей между N-элементами формируется нейросемантическая структура (НСС), которая обладает рядом полезных свойств [ ].

В работах [3,4,5] описаны алгоритмы автоструктуризации, которые из непрерывного информационного потока эффективно выделяют отрезки текста, соответствующие семантическим единицам исследуемой ПО, т.е. автоматическое формирование: 

N-элемент  ↔ "слово-процесс" ПО

Здесь каждому "слову-процессу" ПО соответствует свой  N-элемент и каждый  N‑элемент отображает некоторый устойчивый (быть может даже сложный)  процесс в ПО. Это третье важное свойство элементной базы НСР.

Четвертое важное свойство элементной базы НСР - это анализ N-элементами не только внешних потоков информации, но и внутренних, т.е. анализ того, как меняется физическое состояние самих N-элементов в процессе обработки ими типичной внешней информации. На N-элементах отображается не только внешняя информация, но и процессы работы их самих, см. рис. 7.

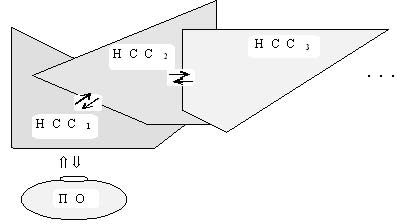
Рис. 7.

Анализ работы иерархической структуры из НСС показал, что в ней возможна организация автоматического формирования R-отношений, которые, как, например, в регуляторе №2, задавались извне. При этом оказалось достаточно двухуровневой иерархической структуры НСС (НСС1 и НСС2). Перейдем к рассмотрению этого механизма.

Свойства N-элемента.

1. Если входной пространственно-временной вектор XT (см. рис. 5) совпадает с пространственно-временным вектором X₀T₀, запаянным в момент его формирования, то N-элемент переходит в активное состояние и на его выходе будет 1*.
2. Если величина свертки, полученной на входном пространственно-временном векторе XT, будет превышать определенный порог P активации для данной области (слоя, НСС), то N-элемент переходит в активное состояние и на его выходе будет * (?).
3. Как только у N-элемента активировался один из входов (желательно один из первых), он переходит в полуактивное состояние и в течение времени T₀ пытается в текущей ситуации "увидеть" свою, за которую он "отвечает". Если ему это удается, то он переходит в активное состояние. Если нет, то он возвращается в ждущий режим.
4. Для каждой области N-элементов характерны свои параметры функционирования. Одними из таких параметров являются порог активации P и время активации внимания T_L  (в течение которого N-элемент пытается продолжить анализ ситуации).  
5. После того как N-элемент активировался (U(t+1) = 1*), величина его возбуждения U(t) падает по экспоненте (U(t+1) = U(t) /τ, например, при τ=2). Это свойство кратковременной памяти. Зная величину U(t) всегда можно определить, когда было предыдущее возбуждение данного N-элемента. Видя все поле величин U(t), можно многократно разворачивать и анализировать последние события.



 

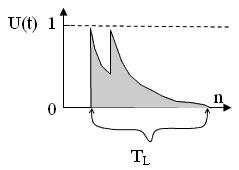
Рис. 8.

 

6. Текстурное свойство N-элемента заключается в "экспоненциальном суммировании" его активностей на интервале T_L (для биологических нейронов  T_L  - не более 10 сек.). После того как N-элемент активировался (U(t+1) = U(t) + 1*) величина его возбуждения U(t) падает по экспоненте (U(t+1) = U(t) / τ, например, при τ = 2). Это свойство текстурности, или счета. Зная величину U(t), всегда можно определить сколько раз активировался N-элемент на интервале T_L.

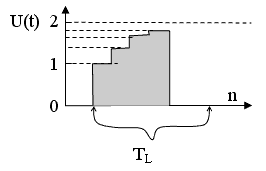
Рис. 9.

Таким образом, например, если U(t) = 1.5, то это значит, что на интервале, не превышающем TL , дважды встречался образ, который "запаян" в данный N-элемент. Если U(t) = 1.75, то трижды и т.д.

Фактически это все свойства, которые необходимы для построения нейросемантического регулятора №3 с требуемым свойством "разумности".

В НСР  №3  получается достаточно сложная, относительно НСР №1 и НСР  №2, структура переработки информации. Тут и анализ внешней ситуации, анализ соответствующего ей изменения состояния нейронов и формирование из всех этих активностей отношений R(X,F), см. рис. 10.

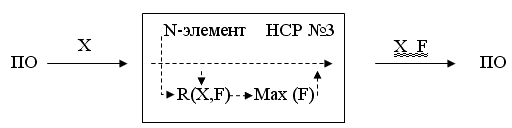
Рис. 10.

В качестве примера использования R-отношений можно рассмотреть задачу - "формирование понятия "абстрактного числа в ИС" (неразрешимую для классического ИИ и легко решаемую биологическими ИС, как высшими животными, так и человеком).

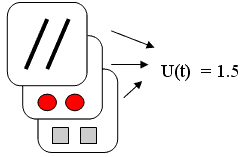
Рис. 11.

Таким образом, если, например, в слое "псевдослов" некоторый N-элемент неоднократно активируется, то уровень активации (*) на нем будет в диапазоне 1*< U(t) < 2*. Если по другому информационному каналу (например, акустическому) будет активация N-элемента с информационным содержанием <два>, <три> или <семь>, то <два>, <три> или <семь> в НСС₂ будет связано с данной величиной U(t+1). И следующий раз, когда будет такое же число распознаваемых объектов (совершенно новых, например, "марсиан-гостей") – ИС выдаст реакцию, что их <два>, <три> или <семь>.

Данным примером мы продемонстрировали один из основных принципов эволюции ИС от простейших форм до ИР – сведение информационных (семантических) характеристик ПО к физическим параметрам ИС.

Второй пример. Рассмотрим задачу по формированию понятия "больше", из "R-школы" НСР №2.

Суть этой задачи заключается в том, что на определенные пары: "1; 2", "2; 3", "3; 4", "4; 5", …  "N; N+1", "1; 5",  "2; 5",   …  "N; N+р" (в каждой паре вторая компонента больше) должен активироваться новый N­элемент, сформировавшийся на вышеперечисленных физических свойствах среды НСС.

1-й шаг. Обучая НСС счету: |; ||; |||; |||; |||||; |||||; |||||||, … , мы получаем N-элемент, который на интервале T_L соединяется с N-элементами "один", "два", "три", … "семь" (см. рис. 9).

2-й шаг. Когда встречается пара, в которой вторая компонента больше первой (напр., "4; 5") мы активируем N-элемент "больше". Если численное соотношение обратное, то активируем N-элемент "меньше". И в случае равенства компонент – "равно".

3-й шаг. В результате у N-элемента "счета" ("от 1 до 7") формируется картина, см. рис. 12.

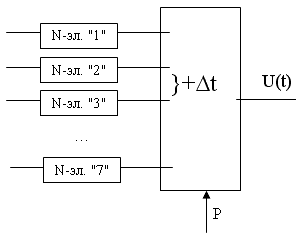
Рис. 12.

4-й шаг. И на текстах НСС:

<3; 4><число><+Δt><больше>

<1; 4><число><+2Δt><больше>

…

<3; 2><число>< -Δt><меньше >

<4; 1><число><-3Δt><меньше >

…

на N-элементах с активацией (U(t)>1) формируются два двувходовых N-элемента:

<+Δt><больше>   и   <-Δt><меньше >

5-й шаг. Теперь, когда у нейрона "счета" активируется +Δt, на одном из сформировавшихся N-элементов образуется U(t) » 0,5, что является максимумом. Соответственно, на N-элемент на втором входе "больше" подается сигнал предвосхищения. Понижая порог р, этот элемент и активируется. Таким образом, в НСС формируются группы N-элементов, которые позволяют ей обучается понятиям "больше"  и "меньше".

Можно привести точную блок-схему НСР №3, аналогичную НСР №1 и НСР №2, но из-за ее громоздкости мы приведем в приложениях только компьютерные результаты.

Этим примером мы показываем формирование на базе только физических параметров НСС новых N-элементов, которые соответствуют  семантическим характеристикам предметной области. Этот пример фактически сводит все отношения из "R-школы" НСР №2 к режиму самообучения ("игры") в НСР №3.

Понятно, что в каждом конкретном случае формирования на НСР №3 отношений из "R-школы" могут возникнуть небольшие непринципиальные затруднения, но также понятно, что они легко преодолимы, если руководствоваться вышеизложенными НСС-принципами и приемами.

Выводы. Эти примеры решают теоретическую проблему построения ИИ.  НСР №3 можно с полным правом назвать "разумным" (НСР №1 – "целеустремленный", НСР №2 –"интеллектуальный").

На всех трех регуляторах можно количественно исследовать различные информационные процессы и давать формальные определения многим понятиям. Нейросемантические регуляторы при своей алгоритмической простоте позволяют формально исследовать очень сложные когнитивные процессы.

СПИСОК  ЛИТЕРАТУРЫ

1. Уосермен Ф. Нейрокомпьютерная техника. М.: Мир. 1992. – 240 с.
2. Sutton R.S., Barto A.G. "Reinforcement Learning: An Introduction". MIT Press, 1998:  http://www-anw.cs.umass.edu/~rich/book/the-book.html
3. Бодякин В.И., Куда идешь, человек? (Основы эволюциологии. Информационный подход). - М. СИНТЕГ, 1998, 332с.   http://www.ipu.ru/stran/bod/monograf.htm
4. Бодякин В.И. Информационные иерархически-сетевые структуры для представления знаний в информационных системах. //Проблемно-ориентированные программы. Модели, интерфейс, обучение: Сб. трудов. – М.: Институт проблем управления, 1990.
5. Бодякин В.И., Чистяков А.А. Ассоциативные информационные структуры и модели памяти, - в сб. Проблемы информатики - материалы конференции "От истории природы к истории общества: "Прошлое в настоящем и будущем", М., 2003.

 Замечания