, 
Самоорганизация информационных развивающихся систем (нейроподобных сред).
г
В.И. Бодякин (ИПУ РАН), И.Б. Петров (МФТИ).E-mail:
BODY@IPU.RSSI.RUОсновой получения формализованных законов, описывающих поведение сложных систем являются вариационные принципы, оптимизирующие поведения системы с целью получения некого результата при минимальных затратах ресурсов.
Классическим и, вероятно, простейшим, с точки зрения теории сложных систем примером, является принцип Гамильтона. Его идея заключается в том, чтобы в качестве фундаментальных основ механика рассматривать не непосредственно дифференциальные уравнения, связывающие механические параметры в каждый момент времени, а некоторые общие
физические принципы, характеризующие движения всей механической системы в целом, на любых временных интервалах. Дифференциальные же соотношения типа уравнений Ньютона,
или Лагранжа
, 
должны быть следствием этих принципов (здесь 
- радиус-вектор материальной точки, 
-силы, действующие на нее, 
- время, 
- функция Лагранжа, 
- обобщенные координаты).
В качестве такого общего для механических систем принципа Гамильтона предложен т.н. принцип наименьшего действия, суть которого заключается в том, что функционал
,
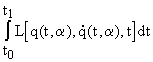называемый действием по Гамильтону, на отрезке 
на прямом пути принимает экстремальное по сравнению с другими, т.н. окольными путями, значение (
- параметр, нулевое значение которого отвечает прямому пути). В терминах вариационного исчисления, уравнения Лагранжа являются дифференциальными уравнениями Эйлера для вариационной задачи
;
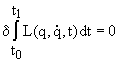при этом прямой путь называется экстремалью.
Можно привести и другие примеры - например, законы отражения (угол падения равен углу отражения) и преломления луча света также являются следствием решения вариационной задачи с условием минимальных затрат времени на его прохождения.
В статике известен закон, в соответствии с которым механическая система принимает положение с минимальной потенциальной энергией, соответствующая задача также является вариационной. В быту нам также часто приходится оптимизировать свои действия, хотя мы этого и не замечаем: например, путь от дома до универсама мы преодолеваем по кратчайшей траектории, но “мозговой компьютер” заставляет нас это делать на уровне подсознания. Аналогичные вариационные принципы существуют и для процессов, описываемых уравнениями в частных производных: уравнение теплопроводности, волновое уравнение, системы уравнений механики и электродинамики сплошных сред. В гидродинамике, как известно, имеют место также процессы самоорганизации, такие как, турбулентность, наступающая после потери устойчивости ламинарного течения, Рэлей - Тэйлоровская неустойчивость, образование т.н. “ячеек Бенара” при нагревании слоя вязкой жидкости с одной стороны и охлаждении его с другой, образование воронки при сливе воды в отверстие; в нелинейной оптике давно известен эффект когерентного излучения, в магнитной гидродинамике - образование т. н. 
- слоев (чередование пиков температуры плазмы), в физической химии - периодические реакции Белоусова - Жаботинского (т.н. контрастные структуры), в биологии - спиралевидные колонии бактерий и т.п. Все эти нелинейные явления являются следствием реализации некоторых вариационных принципов, не все из которых известны науке. Отметим также, что в численных подходах к решению упомянутых задач существует
Во многих задачах физики, химии, биологии, популяционной динамики используется т.н. реакционно-диффузионное уравнение, которое иногда называют основным уравнением теории самоорганизации:
, 
(
- искомая функция; 
- независимые переменные).
Это уравнение, будет иметь эмпирический характер до тех пор, пока не будут найдены соответствующие вариационные принципы самоорганизации физических, химических или биологических систем. Несмотря на кажущуюся сложность, эта задача, тем не менее, должна иметь, решение. Дело в том, что в этом случае открытая система получает энергию и каким-то образом ее преобразует так, что в среде появляются вихри, воронки, спиралевидные волны, периодические структуры и т.п., что во многих случаях описывается известными уравнениями.
Намного более сложной оказывается задача самоорганизации в иерархических информационных, например, антропосоциальных системах. Проблема здесь заключена в том, что наряду с энергетической компонентой, подобные системы получают еще и информационную, и задача оптимизации, в данном случае, усложняется еще и тем, что необходимо учитывать воздействие последней, как на индивидуума, так и на всю социальную группу. Тем не менее, задача самоорганизации, которая, в конечном итоге должна быть сведена к некоторой вариационной, эмпирически все-таки должна иметь решение. Так, например, известно, что существуют следующие принципы функционирования и развития таких систем:
- неравновесное состояние, как условие динамического функционирования и, соответственно, развития системы;
- наличие, как упорядоченности, так и хаотической компоненты;
- компенсация, или минимизация последствий внешнего воздействия;
- экспансия, т.е. расширение системы за счет других, как следствие неравновесности более общей системы;
- иерархическое строение, как структурообразование “по вертикали”;
- функциональное структурообразование;
- наличие двух компонент: материальной и информационной;
- наличие памяти (банка данных) системы; в теории наследственных сред (т.е. сред с памятью) известен аналог, простейшая модель которого, может быть записана в следующем виде:
,
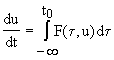где - искомая функция, описывающая поведение системы; таким образом, если мы хотим ввести память элемента нейроподобной среды, то в этом случае необходимо использовать подобные наследственные модели;
- возможность неоднозначного решения задачи, например, минимизации внешнего воздействия, как индивидуумом (т.н. “свобода выбора”), так и социальной группой; однако, чем больше группа, тем меньше вариантов выбора; так, например, поведение больших социальных групп в ряде случаев может быть описано уравнениями механики сплошных сред (без учета их иерархического строения).
Для описания иерархических систем наиболее естественным представляется использование моделей нейроподобных сред, хотя, разумеется, для формализованного описания тех или иных частных процессов можно с успехом использовать иные методы нелинейной динамики (разностные отображения, нелинейные дифференциальные уравнения, клеточные автоматы и др.). Заметим также, что постулируемая иерархичность систем, в свою очередь, также является следствием реализации более общего вариационного принципа. В этом сказывается и иерархическое строение самих моделей: одни модели являются следствием других, более общих, и т.д. Например, для моделей механики сплошных сред, такая иерархическая цепочка имеет вид:
|
Вариационные уравнения механики сплошных сред |
|||||||||
|
Ї |
|||||||||
|
Система дифференциальных уравнений в частных производных механики сплошных сред |
|||||||||
|
Ї Ѕ Ї Ѕ Ї |
|||||||||
|
Уравнение Эйлера сжимаемого невязкого газа |
|
Уравнение Навье-Стокса для сжимаемого вязкого газа |
|
Уравнения механики деформируемого твердого тела |
|||||
|
Ї Ѕ Ї Ѕ Ї Ї |
|||||||||
|
Уравнение несжимаемого газа |
|
Уравнение пограничного слоя вязкого газа |
|
Уравнение Ламэ для упругого тела |
|
Уравнение Прандтля-Рейсса для упругопластического тела |
|||
|
_ _ _ _ Ї _ _ Ѕ _ _ _ Ї _ _ Ѕ _ _ _ Ї _ _ _ _ _ _ _ Ї _ _ |
|||||||||
|
|
|||||||||
|
Уравнения Рейнольда для турбулентных течений |
|
Уравнение магнитной гидродинамики (с системой уравнений Максвелла) |
|||||||
|
_ _ _ _ __ _ Ї _ _ _ _ _ _ _ _ _ _ _ _ _ _ _Ї _ _ _ _ _ |
|||||||||
Для антропосоциальных систем подобных схема будет выглядеть существенно сложнее, т.к. необходимо учитывать демографические, экономические, политологические, этнические, процессы; наличие интеллектуальных, культурных, исторических ценной, этнические особенности и т.п. Тем не менее, изучение достаточно общих принципов, управляющих подобными системами, делает, в определенной степени, эту задачу разрешимой.
Кроме того, базируясь на принципах синергетической теории, мы предполагаем, что нейроподобная среда, пропуская через себя информационные потоки, проявляет свойства самоорганизации, изучив которые, можно прогнозировать ее поведение.
При этом явления самоорганизации среды, несут общий компенсационный характер, который можно выразить следующим обобщенным законом: всякое воздействие на "среду-структуру", если оно ее не разрушает, приводит в ней к изменениям, частично компенсирующим исходное возмущение.
Данный закон есть проявление функции отражения "как всеобщего свойства материи" (например, принцип Ле Шателье в химии - "химические реакции протекают в направлении, уменьшающим воздействие внешнего фактора ми сохраняющим стабильность системы" и др.). При этом из возможного множества отражательных процессов (управлений) на передний план выступает только один, в соответствии с принципом Гамильтона, и в соответствии, с минимумом действия. Таким образом, философская категория отражения и кибернетическое управление (отрицательная обратная связь) тесно смыкаются по генезису.
Известно, например, что по мере нагревания тонкого слоя жидкости, наступает момент, когда из хаотических конвективных потоков рождается регулярная теплопроводящая структура, так называемые “ячейки Бенара” [1]. Ответная регулярная структура повышает эффективность переноса тепла, "адаптируя" проводящую среду под внешнее воздействие. Аналогичные процессы происходят и в более сложных (структурно и функционально) однородных информационных средах. Так, например, нейроподобные среды, как и социальные, пропуская через себя информационные потоки, проявляют аналогичные свойства самоорганизации, но с отличительным многообразием, в соответствии с их параметрической сложностью, см. рис. 1.
Можно попытаться выделить основные параметры для моделирования синергетических процессов в физических, в нейроподобных и в социальных средах. По аналогии с физической моделью, можно провести параллели: "мощность информационного и теплового потоков", “градиент в социально-экономических температурах”, "граничные условия, как культурно-исторические особенности” и пр. Моделирование социальных сред показано в [3], и в задачу данной статьи входит рассмотрение только аналогии физических и нейроподобных сред [3,4].
Отметим параллели и отличия этих двух моделей:
– внешние возмущения (G, I) вызывают изменения в структуре сред;
– среды обладают памятью:
D t = t - для физической среды (время прохождения G-фронта возмущения через нее); и D t » Ґ - для информационной среды (как для состоящей из бистабильных /нейроподобных/ элементов);– после формирования структуры в средах возрастает проводимость, или же уменьшается сопротивление прохождению возмущению (G, I), это так называемый коэффициент компрессии - P. Для физической среды это константа P = С (С ~ 1); для информационной среды P >> 1;
– в информационных средах четко выделяется иерархичность структур, их псевдофрактальность, тогда как для физических сред она слабо выражена;
– если для физических сред геометрическая структура задается почти однозначно геометрией среды и структурой (образа) возмущения - G (шестигранные "ячейки Бенара"), то для информационных сред существует множество геометрических различных, но функционально изоморфных структур, поэтому аналогом геометрической формы можно рассматривать устойчивые функциональные структуры, которые однозначно определяются числом операций вызываемых воздействием - I. Отметим, что и в физических средах, появление регулярных структур, также ведет к уменьшению числа столкновений-операций частиц (уменьшение сопротивления среды). Т.е. о качестве структуризации информационных сред говорит параметр Р - "число операций в нейроподобных элементах". Под операцией будем понимать процесс прохождения единичного сигнала между парой нейроподобных элементов;
Рассмотрим с позиции минимизации допустимые реакции нейроподобной среды (
D S - количественное приращение и возможное качественное видоизменение структуры) на внешнее возмущение I(t2- t1).Напомним, исходные условия:
Первые следствия из анализа исходных условий:
– преобразование I(t)
– структура S должна быть эффективной для идентификации возмущений I(t), т.е. необходимо организовать параллельную работу нейроподобных элементов структуры;
Для конструкции среды, удовлетворяющей вышеперечисленным условиям можно предложить следующее:
– основной элемент активный среды (нейроподобный N-элемент) обратимо обрабатывающий сигнал I(t). N-элемент имеет k пронумерованных от 1 до k входов и один выход. N-элемент может находится в четырех состояниях: - резерва, отображения, ассоциативной идентификации и обратного обращения образа (N а I'(tk-t1)). В режиме отображения I(t) а S свободные входы, начиная с 1-го до k-й образуют вектор-образ пространственно-временных (x1t1; x2t2; ... xktk;) связей, отображающий некоторый фрагмент I(tk-t1), см. рис. 2.
В режиме обратного обращения образа, N-элемент генерирует пространственно-временной образ (x
1t1; x2t2; ... xktk;) или его заключительную часть ("опережающее отражение").– нейроподобная среда из N-элементов
имеет регулярную иерархическую организацию, см. рис 3.Структуру нейроподобной среды удобно представить исходя из лингвистической метафоры. Первый слой - "алфавит": "слоги" (или "символы", при k=1), второй слой - "слова", третий - "фразы" и т.д. Причем, "слова" состоят из "слогов", - "фразы" из "слов" и т.д. многодольный граф. Понятно, что любой текст - I(t) легко разложим в данной среде на составляющие его образы ("слоги", "слова", "фразы" и т.д.). Весь процесс отображения - это растущий многодольный L-граф, см. рис.4.
Естественно, что говоря о конструктивных особенностях среды необходимо постоянно иметь ввиду свойства и характеристики самого источника сигнала I(t) из предметной области (ПО).
Первое, это по видимому то, что процессы (законы ПО), порождающие I(t) должны иметь "псевдофрактальную природу" для возможности самоописания в самой ПО. Т.е., должен существовать небольшой базис из законов-операторов (F), порождающий все многообразие образов в I(t), только так можно записать сами законы (F) и I(t) в одной внешней среде (ПО).
Второе, это то, что процессы ПО, отображаемые в последовательности I(t), должны подчинятся принципу причинности и принципу подобия
[3].Еще одна особенность, говоря среда, а не система, мы подчеркиваем их принципиальное различие, если система, что особенно характерно для технических систем, - это особые пространственно выделенные области (точки запуска и пр.), то активная среда - это особые функционально выделенные структуры и процессы на общей функциональной однородности.
Псевдофрактальность ПО хорошо отображается иерархической организацией N-элементов, см. рис. 4. Емкость информационного содержания (фрагмент I(t
2-t1)) N-элементов от слоя (i) к слою (i+1) растет в k раз, соответственно, емкость N-элементов m-го слоя определяется как mk (степенная функция). При этом нелинейность, как коэффициент компрессии отображается как - P » logk (I(t)), при t ® Ґ , см. рис 5.Вообще, "поведение" коэффициента компрессии качественно характеризует механизмы отображения ИС. Если значение P
» const (» 1ё 1000), то такие методы отображения можно охарактеризовать как "статистические". Если же значение P - монотонно возрастает с ростом длины I(t), - то как "самоорганизующиеся".N-элементы в слое ИС независимы и функционируют параллельно, см. рис.3 и рис. 4. В процессе отображения I(t) в ИС каждый N-элемент соединяется связями с N-элементами нижерасположенного уровня. Связи, посредством терминального слоя N-элементов (алфавитом) фактически и определяют информационное содержание каждого N-элемента - I(t
j+1-tj). Соответственно, если на вход ИС поступает последовательность, соответствующая содержанию некоторого N-элемента, то он переходит в активное состояние, в соответствии с близостью к его информационному содержанию. Из всего слоя выделяется один N-элемент, имеющий максимальную активность и образует связь с N-элементом вышележащего уровня ИС. Это принцип ассоциативной работы ИС. За один такт обрабатываются N-элементы в слое и за один обобщенный такт ИС выполняется полная ассоциативная обработка входной информации во всех слоях. Причем, время идентификации (T) в ИС не зависит от числа обрабатываемых N-элементов, а определяется только длиной идентифицируемой символьной последовательности I(tj+1-tj) во входном потоке, см. рис 5.Независимость и параллельность функционирования N-элементов приводит к тому, что надежность (Q) функционирования всей ИС много больше чем надежность (q) отдельных ее N-элементов.
Q» (1-q)ФП, где ФП - среднее число параллельных траекторий активации N-элементов в процессе идентификации, см. рис 5.Еще одна особенность процесса отображения I(t) в ИС это разбиение I(t) на образы:
I(t) = I(t2-t1) + I(t3-t2) + ... + I(tj+1-tj) + ... + I(tn+1-tn), где знак + - конкатенация. Фактическое число всевозможных разбиений (t1; t2; ... tj; ... tn), практически, бесконечно, но только одно разбиение (t1; t2; ... tj; ... tn) дает максимальное значение компрессии. Характерно, что в этом случае, отображению каждого фрактального процесса в ПО - I(tj+1-tj)ПО - соответствует информационное содержание отдельного N-элемента - I(tj+1-tj)ИС. Качество данного соответствия отображается отношением суммы I(tj+1-tj)ИС соответствующих I(tj+1-tj)ПО к сумме всех N-элементов ИС. Ориентируясь на значение компрессии (Р) в процессе формирования ИС, как на критерий корректности структуризации удается осуществлять процесс сходящийся к разбиению (t1;t2; ... tj; ... tn), который мы назвали автоструктуризацией, см. рис.6.Исходя из псевдофрактальной природы законов-операторов (F) в самой ПО, можно усилить это свойство в ИС. Если над "ИС-первого порядка" (см. рис. 4)
сформировать на таких же принципах "ИС-второго порядка", за тем лишь исключением, что в ней будет отображаться не I(t), а процессы в "ИС-первого порядка", и тогда в ней уже будет отображаться не фактографическая последовательность I(t), а причинно-следственные правила ПО активации N-элементов "ИС-первого порядка". При этом коэффициент компрессии Р многократно возрастает, так как если обозначить основную функцию ИС как "опережающее отражение", то отображение I(t) в ИС уже будет не фактографическое, а функциональное, см. рис. 7.Можно предположить, что можно построить "ИС
F порядка" которое будет изоморфна исходным F-законам-операторам ПО. При этом компрессия будет максимально возможной, и ИС будет обладать возможностью "полного опережающего отражения" I(t).В заключении хотелось бы опять вернуться к началу статьи. Активные среды с достаточной функциональной организованностью (например, нейросемантические структуры) способны сами отобразить, причем самым эффективным способом возмущения внешней (менее активной) среды. Механизмы этого процесса вполне понятны и могут быть описаны более формальным способом, а главное? смоделированы на ЭВМ.
Соответственно, возможно понять и тенденции эволюционирования сложных сред: биологических нейронных структур, различных социальных образований и пр.
Литература:
